Case Study: Replicating Mishra et al. (2020)

Introduction

This vignette demonstrates how to replicate the analysis from Mishra et al. (2020) of COVID-19 transmission dynamics in South Korea using EpiAwareR. This case study showcases the compositional modelling approach by building a complete epidemiological model from three reusable components.

The analysis estimates the time-varying reproduction number ( $R_t$ ) using:

AR(2) latent process for smooth evolution of log $R_t$
Renewal equation for infection dynamics
Negative binomial observation model for overdispersed case counts

Data Preparation

We use the actual South Korea COVID-19 data from the preprint, which is included in the package. The data comes from the covidregionaldata R package and contains daily confirmed cases from January to July 2020.

# Load South Korea COVID-19 data
data_path <- system.file("extdata", "south_korea_data.csv", package = "EpiAwareR")
south_korea <- read.csv(data_path)
south_korea$date <- as.Date(south_korea$date)

# Prepare full dataset - tspan will select the window
# Column must be named 'y_t' for EpiAware
full_data <- data.frame(
  date = south_korea$date,
  y_t = south_korea$cases_new
)

# Preview the training window (days 45-80)
# This corresponds to Feb 13 - Mar 19, 2020 (the main epidemic wave)
cat("Training window (tspan 45-80):\n")
#> Training window (tspan 45-80):
print(full_data[45:80, ])
#>          date y_t
#> 45 2020-02-13   0
#> 46 2020-02-14   0
#> 47 2020-02-15   0
#> 48 2020-02-16   1
#> 49 2020-02-17   1
#> 50 2020-02-18   1
#> 51 2020-02-19  15
#> 52 2020-02-20  34
#> 53 2020-02-21  75
#> 54 2020-02-22 190
#> 55 2020-02-23 256
#> 56 2020-02-24 161
#> 57 2020-02-25 130
#> 58 2020-02-26 254
#> 59 2020-02-27 449
#> 60 2020-02-28 427
#> 61 2020-02-29 909
#> 62 2020-03-01 595
#> 63 2020-03-02 686
#> 64 2020-03-03 600
#> 65 2020-03-04 516
#> 66 2020-03-05 438
#> 67 2020-03-06 518
#> 68 2020-03-07 483
#> 69 2020-03-08 367
#> 70 2020-03-09 248
#> 71 2020-03-10 131
#> 72 2020-03-11 242
#> 73 2020-03-12 114
#> 74 2020-03-13 110
#> 75 2020-03-14 107
#> 76 2020-03-15  76
#> 77 2020-03-16  74
#> 78 2020-03-17  84
#> 79 2020-03-18  93
#> 80 2020-03-19 152

# Plot the training data
plot(full_data$date[45:80], full_data$y_t[45:80], type = "b",
     xlab = "Date", ylab = "Daily Cases",
     main = "South Korea COVID-19 Cases (Feb 13 - Mar 19, 2020)")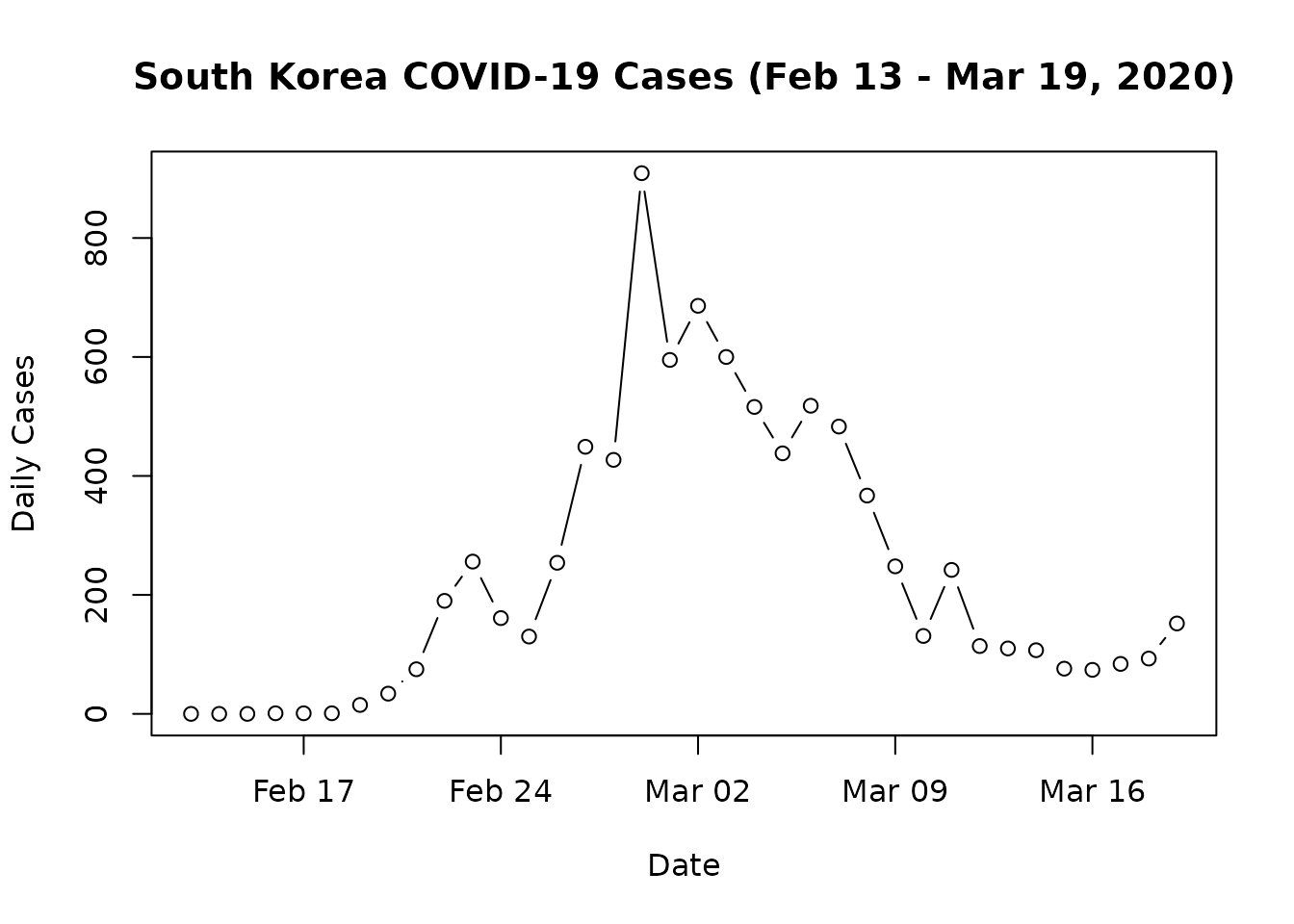

Model Components

1. Latent Process: AR(2) Model

The AR(2) process models the evolution of log $R_t$ over time with temporal autocorrelation:

$\log R_t = \phi_1 \log R_{t-1} + \phi_2 \log R_{t-2} + \epsilon_t$

where $\epsilon_t \sim \text{Normal}(0, \sigma^2)$ .

ar2 <- AR(
  order = 2,
  damp_priors = list(
    truncnorm(0.1, 0.05, 0, 1), # ρ₁: Second-order coefficient
    truncnorm(0.8, 0.05, 0, 1)  # ρ₂: First-order (strong autocorrelation)
  ),
  init_priors = list(
    norm(-1.0, 0.1), # Initial value for lag 1
    norm(-1.0, 0.5)  # Initial value for lag 2
  ),
  std_prior = halfnorm(0.5) # σ: Innovation standard deviation
)
#> Julia version 1.11.8 at location /opt/hostedtoolcache/julia/1.11.8/x64/bin will be used.
#> Loading setup script for JuliaCall...
#> Finish loading setup script for JuliaCall.
#> EpiAware Julia backend loaded successfully

print(ar2)
#> <EpiAware AR(2) Latent Model>
#>   Damping priors: 2 
#>   Init priors: 2 
#>   Innovation std prior: specified

Prior choices (from Mishra et al. 2020):

First-order damping coefficient ρ₂ centered at 0.8 reflects strong autocorrelation in log Rt
Second-order damping coefficient ρ₁ centered at 0.1 for smooth dynamics
Initial values centered at -1 on log scale (Rt ≈ 0.37 initially)
Innovation std of 0.5 allows flexibility in Rt changes

2. Infection Model: Renewal Equation

The renewal equation models new infections based on past infections and generation time:

$I_t = R_t \sum_{s=1}^{t} I_{t-s} \cdot g_s$

where $g_s$ is the discretized generation time distribution.

renewal <- Renewal(
  gen_distribution = gamma_dist(6.5, 0.62), # Shape and scale parameters
  initialisation_prior = norm(log(1.0), 1.0) # Prior on initial log infections (wide)
)

print(renewal)
#> <EpiAware Renewal Infection Model>
#>   Generation distribution: Gamma 
#>   Initialisation prior: specified

Key parameters:

Generation time: Mean ~6.5 days (typical for COVID-19 in early 2020)
Gamma distribution allows flexible shape
Initial infections seeded near 1 with wide prior (sd=1.0 on log scale)

3. Observation Model: Negative Binomial

Links latent infections to observed case counts with overdispersion:

$Y_t \sim \text{NegBinom}(\mu = I_t, \phi)$

where $\phi$ controls overdispersion (clustering).

# The preprint fixes cluster_factor to 0.25
# We approximate this with a tight truncated normal prior
negbin <- NegativeBinomialError(
  cluster_factor_prior = truncnorm(0.25, 0.01, 0, 1)
)

print(negbin)
#> <EpiAware Negative Binomial Observation Model>
#>   Cluster factor prior: truncated(Normal(mean, sd), lower, upper)

Parameterization:

Cluster factor = $\sqrt{1/\phi}$ (coefficient of variation)
Fixed to 0.25 (via tight prior) as in the preprint
More interpretable than directly specifying $\phi$

Compose and Fit

Create Complete Model

model <- EpiProblem(
  epi_model = renewal,
  latent_model = ar2,
  observation_model = negbin,
  tspan = c(45, 80) # Exact tspan from preprint (Feb 13 - Mar 19, 2020)
)

print(model)
#> <EpiAware Epidemiological Model>
#>   Time span: 45 to 80 
#>   Components:
#>     - Infection model: epiaware_renewal 
#>     - Latent model: epiaware_ar 
#>     - Observation model: epiaware_negbin

The EpiProblem combines components into a joint Bayesian model with automatic validation. The tspan = c(45, 80) selects days 45-80 from the full dataset, matching the preprint exactly.

Bayesian Inference

We use NUTS (No-U-Turn Sampler) with Pathfinder initialization for posterior inference:

results <- fit(
  model = model,
  data = full_data, # Pass full dataset; tspan selects the window
  method = nuts_sampler(
    warmup = 1000, # Adaptation iterations
    draws = 2000, # Posterior samples per chain (matches preprint)
    chains = 4 # Independent chains for convergence assessment
  )
)
#> Generating Turing.jl model...
#> Running NUTS sampling...
#>   Chains: 4
#>   Warmup: 1000
#>   Draws: 2000
#>   Running Pathfinder initialization...
#>   Pathfinder initialization failed, using default initialization...
#> Processing results...

Note: Fitting typically takes 2-5 minutes on modern hardware.

Results

Convergence Diagnostics

print(results)
#> <EpiAware Model Fit>
#> 
#> Model:
#>   Time span: 45 to 80 
#>   Infection model: epiaware_renewal 
#>   Latent model: epiaware_ar 
#>   Observation model: epiaware_negbin 
#> 
#> Sampling:
#>   Method: NUTS
#>   Chains: 4 
#>   Draws: 2000 (per chain)
#> 
#> Convergence:
#>   Max Rhat: 1.054 
#>   Min ESS (bulk): 71 
#>   Warning: Some parameters have ESS < 100
#> 
#> Use summary() for parameter estimates
#> Use plot() to visualize results

Check for:

Rhat < 1.1: Chains have converged to the same distribution
ESS > 100: Sufficient effective sample size for inference
No divergent transitions: NUTS is exploring the posterior efficiently

Parameter Summaries

# Detailed posterior summaries
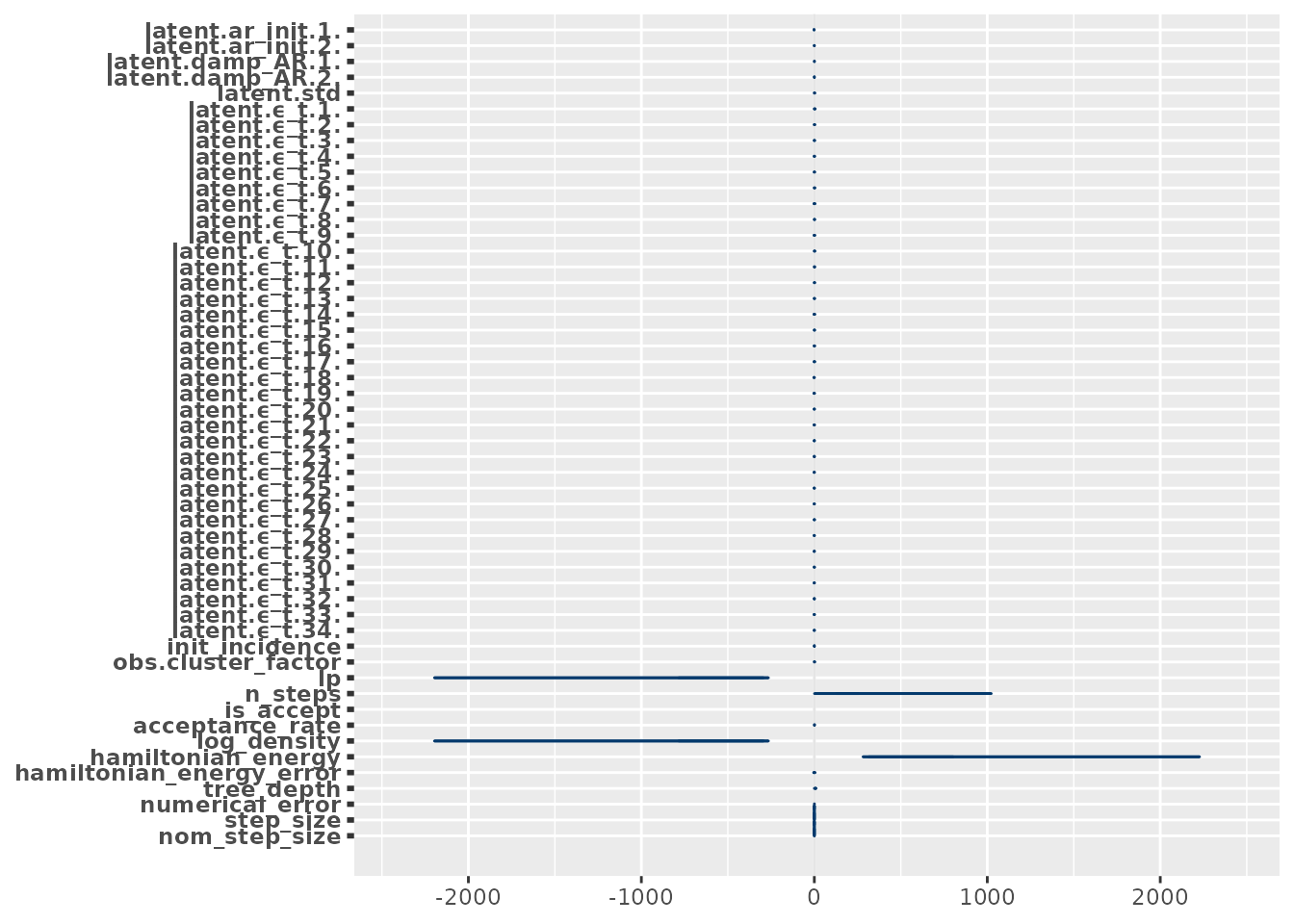
summary(results)
#> # A tibble: 53 × 10
#>    variable    mean  median     sd    mad      q5    q95  rhat ess_bulk ess_tail
#>    <chr>      <dbl>   <dbl>  <dbl>  <dbl>   <dbl>  <dbl> <dbl>    <dbl>    <dbl>
#>  1 latent.… -0.994  -0.994  0.100  0.102  -1.16   -0.830  1.00   11528.    5107.
#>  2 latent.… -0.656  -0.648  0.469  0.473  -1.44    0.107  1.00    8623.    5223.
#>  3 latent.…  0.0839  0.0832 0.0397 0.0416  0.0200  0.152  1.00    5040.    3202.
#>  4 latent.…  0.809   0.808  0.0445 0.0442  0.736   0.881  1.00    3717.    1790.
#>  5 latent.…  0.556   0.548  0.0894 0.0874  0.424   0.713  1.00    4002.    4909.
#>  6 latent.…  0.982   0.990  0.892  0.880  -0.479   2.43   1.00    9452.    5536.
#>  7 latent.…  1.37    1.36   0.890  0.891  -0.0831  2.82   1.00    9555.    4553.
#>  8 latent.…  1.24    1.24   0.902  0.902  -0.248   2.75   1.00   11309.    6087.
#>  9 latent.…  1.18    1.17   0.893  0.882  -0.283   2.67   1.00   10868.    5106.
#> 10 latent.…  2.16    2.16   0.816  0.822   0.820   3.52   1.00    9389.    5849.
#> # ℹ 43 more rows

Key parameters to examine:

AR damping coefficients ( $\phi_1$ , $\phi_2$ ): Autocorrelation strength
Innovation std ( $\sigma$ ): Variability in $R_t$ changes
Cluster factor: Degree of case count overdispersion
Initial infections: Epidemic seeding

Visualization

# Time-varying reproduction number with credible intervals
plot(results, type = "Rt")


# Observed vs predicted case counts
plot(results, type = "cases")


# Posterior distributions for key parameters
plot(results, type = "posterior")

Model Comparisons

Comparing Latent Processes

Test sensitivity to AR order:

# AR(1) alternative - strong autocorrelation like AR(2)
ar1 <- AR(
  order = 1,
  damp_priors = list(truncnorm(0.8, 0.05, 0, 1)),  # High autocorrelation
  init_priors = list(norm(-1.0, 0.5)),
  std_prior = halfnorm(0.5)
)

model_ar1 <- EpiProblem(
  epi_model = renewal,
  latent_model = ar1,
  observation_model = negbin,
  tspan = c(45, 80)
)

results_ar1 <- fit(model_ar1, data = full_data)
#> Generating Turing.jl model...
#> Running NUTS sampling...
#>   Chains: 4
#>   Warmup: 1000
#>   Draws: 1000
#>   Running Pathfinder initialization...
#>   Pathfinder initialization failed, using default initialization...
#> Processing results...

Compare the $R_t$ estimates from both models:

library(ggplot2)
library(patchwork)

p_ar2 <- plot(results, type = "Rt") +
  ggtitle("AR(2) Model") +
  coord_cartesian(ylim = c(0, 6))

p_ar1 <- plot(results_ar1, type = "Rt") +
  ggtitle("AR(1) Model") +
  coord_cartesian(ylim = c(0, 6))

p_ar2 + p_ar1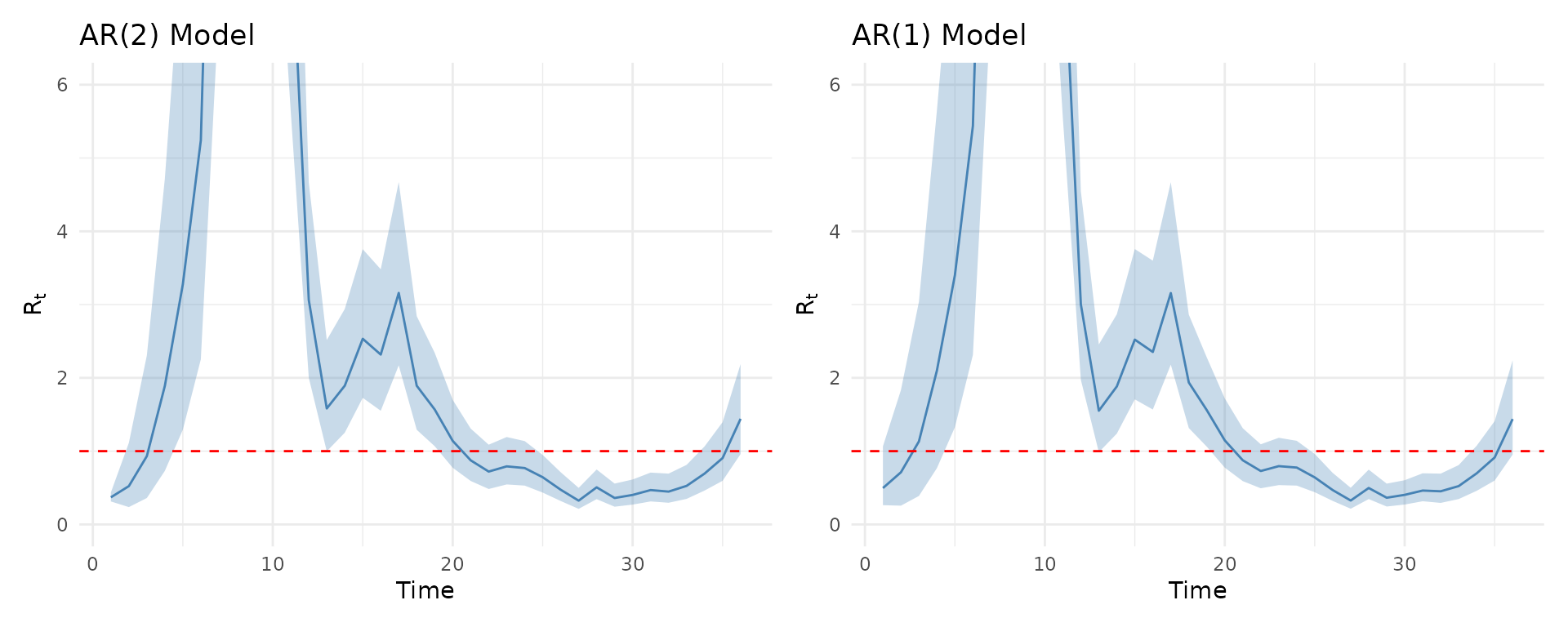

The AR(2) model typically produces smoother $R_t$ trajectories due to the additional lag term, while AR(1) may show more rapid fluctuations.

Adding Observation Delays

Account for incubation and reporting delays:

# Incubation period (~5 days)
obs_incubation <- LatentDelay(
  model = negbin,
  delay_distribution = lognorm(1.6, 0.42)
)

# Reporting delay (~2 days)
obs_full <- LatentDelay(
  model = obs_incubation,
  delay_distribution = lognorm(0.58, 0.47)
)

model_delays <- EpiProblem(
  epi_model = renewal,
  latent_model = ar2,
  observation_model = obs_full,
  tspan = c(45, 80)
)

results_delays <- fit(model_delays, data = full_data)
#> Generating Turing.jl model...
#> Running NUTS sampling...
#>   Chains: 4
#>   Warmup: 1000
#>   Draws: 1000
#>   Running Pathfinder initialization...
#>   Pathfinder initialization failed, using default initialization...
#> Processing results...

Compare models with and without observation delays:

p_no_delay <- plot(results, type = "Rt") +
  ggtitle("Without Delays") +
  coord_cartesian(ylim = c(0, 6))

p_delay <- plot(results_delays, type = "Rt") +
  ggtitle("With Incubation + Reporting Delays") +
  coord_cartesian(ylim = c(0, 6))

p_no_delay + p_delay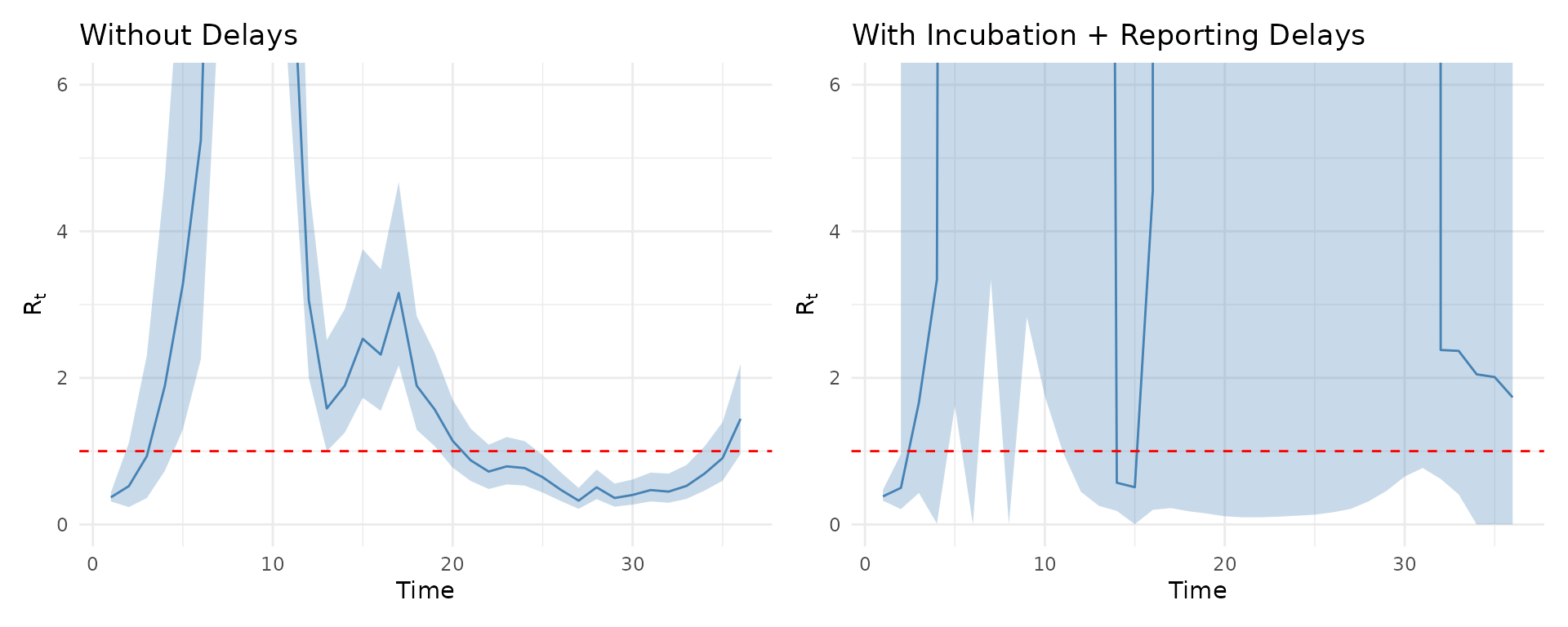

Accounting for delays shifts the $R_t$ trajectory earlier in time, as infections precede observed cases.

Interpretation

The Mishra et al. (2020) analysis demonstrated:

Flexible $R_t$ estimation: AR(2) captures both smooth trends and rapid changes
Uncertainty quantification: Bayesian credible intervals reflect parameter uncertainty
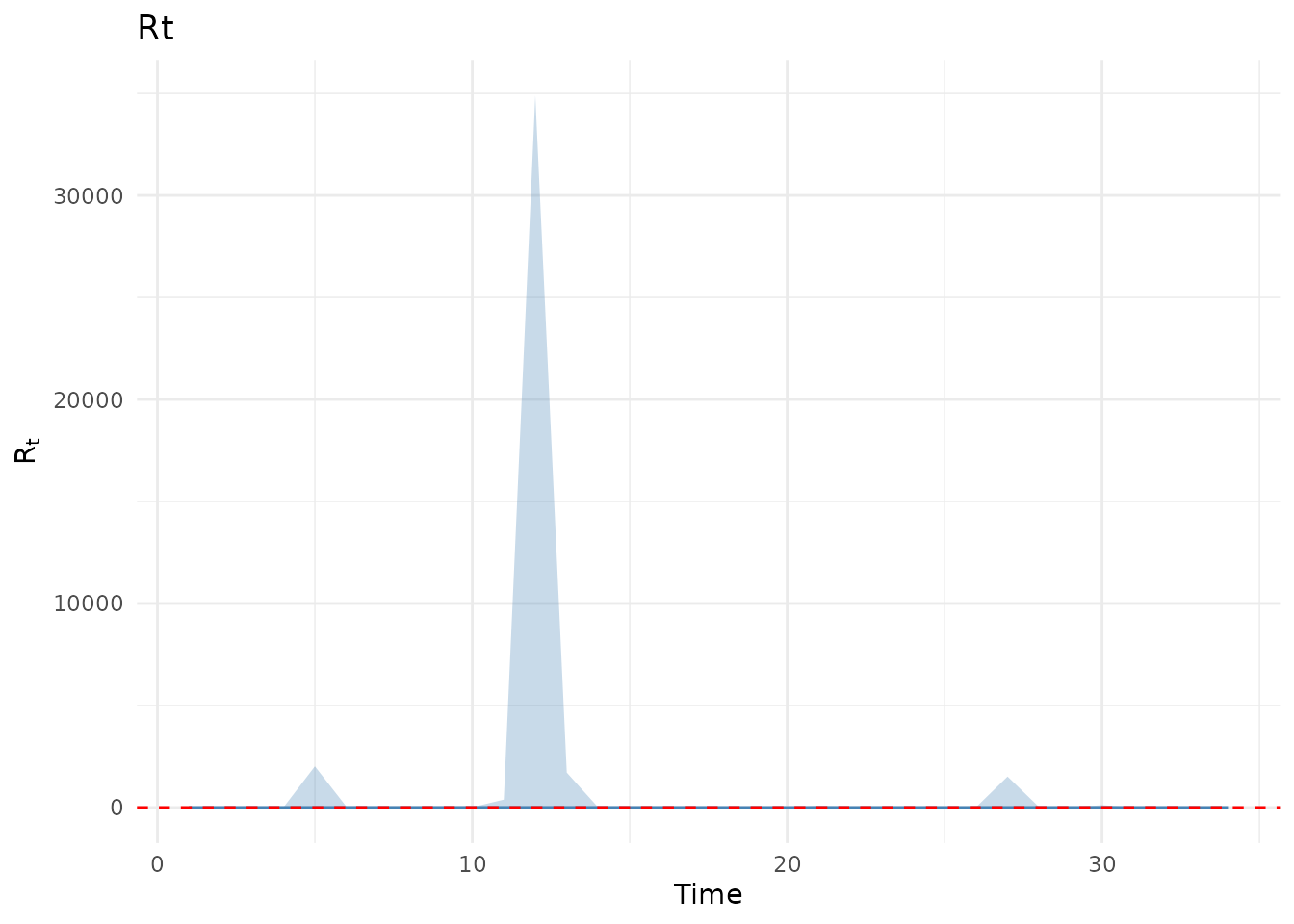
Intervention detection: Sharp decline in $R_t$ coincides with public health measures
Compositional flexibility: Easy to test alternative assumptions (AR order, delays)

Key Findings

Initial $R_t \approx 2.5$ : Rapid exponential growth phase
Post-intervention $R_t < 1$ : Control achieved through distancing measures
Moderate overdispersion: Case counts show clustering but not extreme variance
Good model fit: Posterior predictive checks show data within credible intervals

Extensions

Try modifying the analysis:

Different priors: Test sensitivity to prior choices
Alternative latent models: MA, random walk, spline models
Stratification: Separate models by age group or region
Forecast evaluation: Hold-out validation of predictive performance

References

Mishra, S., Berah, T., Mellan, T. A., et al. (2020). On the derivation of the renewal equation from an age-dependent branching process: an epidemic modelling perspective. arXiv preprint arXiv:2006.16487.

Session Info

sessionInfo()
#> R version 4.5.2 (2025-10-31)
#> Platform: x86_64-pc-linux-gnu
#> Running under: Ubuntu 24.04.3 LTS
#> 
#> Matrix products: default
#> BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
#> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so;  LAPACK version 3.12.0
#> 
#> locale:
#>  [1] LC_CTYPE=C.UTF-8          LC_NUMERIC=C             
#>  [3] LC_TIME=C.UTF-8           LC_COLLATE=C.UTF-8       
#>  [5] LC_MONETARY=C.UTF-8       LC_MESSAGES=C.UTF-8      
#>  [7] LC_PAPER=C.UTF-8          LC_NAME=C.UTF-8          
#>  [9] LC_ADDRESS=C.UTF-8        LC_TELEPHONE=C.UTF-8     
#> [11] LC_MEASUREMENT=C.UTF-8    LC_IDENTIFICATION=C.UTF-8
#> 
#> time zone: UTC
#> tzcode source: system (glibc)
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] patchwork_1.3.2      ggplot2_4.0.1        EpiAwareR_0.1.0.9000
#> 
#> loaded via a namespace (and not attached):
#>  [1] tensorA_0.36.2.1     sass_0.4.10          utf8_1.2.6          
#>  [4] generics_0.1.4       stringi_1.8.7        digest_0.6.39       
#>  [7] magrittr_2.0.4       evaluate_1.0.5       grid_4.5.2          
#> [10] RColorBrewer_1.1-3   fastmap_1.2.0        plyr_1.8.9          
#> [13] jsonlite_2.0.0       backports_1.5.0      scales_1.4.0        
#> [16] textshaping_1.0.4    jquerylib_0.1.4      abind_1.4-8         
#> [19] cli_3.6.5            rlang_1.1.7          withr_3.0.2         
#> [22] cachem_1.1.0         yaml_2.3.12          tools_4.5.2         
#> [25] reshape2_1.4.5       checkmate_2.3.3      dplyr_1.1.4         
#> [28] JuliaCall_0.17.6     vctrs_0.7.1          posterior_1.6.1     
#> [31] R6_2.6.1             ggridges_0.5.7       matrixStats_1.5.0   
#> [34] lifecycle_1.0.5      stringr_1.6.0        fs_1.6.6            
#> [37] ragg_1.5.0           pkgconfig_2.0.3      desc_1.4.3          
#> [40] pkgdown_2.2.0        pillar_1.11.1        bslib_0.9.0         
#> [43] gtable_0.3.6         glue_1.8.0           Rcpp_1.1.1          
#> [46] systemfonts_1.3.1    xfun_0.56            tibble_3.3.1        
#> [49] tidyselect_1.2.1     knitr_1.51           farver_2.1.2        
#> [52] bayesplot_1.15.0     htmltools_0.5.9      rmarkdown_2.30      
#> [55] labeling_0.4.3       compiler_4.5.2       S7_0.2.1            
#> [58] distributional_0.6.0

Sebastian Funk

2026-01-26